

Si dice che un colore ha l'opposizione favorevole (o la mossa) se, quando i pezzi avversari si fronteggiano, l'altro è costretto a indietreggiare. Nei finali, quando sono presenti pochi pezzi, l'opposizione favorevole può far guadagnare tempi e spazi decisivi determinando il risultato, come si vedrà nello studio dei finali teorici.
 Nella
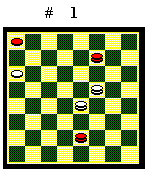
posizione del Diagramma 1, chi deve muovere è costretto ad
indietreggiare, altrimenti perde un pezzo. Pertanto, chi muove non ha la
mossa.
Nella
posizione del Diagramma 1, chi deve muovere è costretto ad
indietreggiare, altrimenti perde un pezzo. Pertanto, chi muove non ha la
mossa.
 Nella
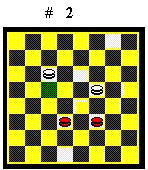
posizione del Diagramma 2, se muove il Bianco può giocare
10-14, poi il Nero deve indietreggiare. Se muove il Nero può giocare
22-18, poi il Bianco deve indietreggiare. Pertanto, chi muove ha la mossa.
Nella
posizione del Diagramma 2, se muove il Bianco può giocare
10-14, poi il Nero deve indietreggiare. Se muove il Nero può giocare
22-18, poi il Bianco deve indietreggiare. Pertanto, chi muove ha la mossa.
Naturalmente il concetto vale se i due colori hanno lo stesso numero di
pezzi, altrimenti, quando i pezzi si fronteggiano, chi ha un pezzo in più
può muoverlo ed obbligare l'avversario ad indietreggiare in ogni
caso.
Per il calcolo della mossa in posizioni più complesse conviene dividere mentalmente i pezzi, indipendentemente dal colore, in coppie. Quindi distinguere le coppie in pari o dispari a seconda che il numero di caselle che separano i due pezzi sia rispettivamente pari o dispari. Se si ha un numero dispari di coppie pari, chi muove ha la mossa; se si ha un numero pari di coppie pari, chi muove non ha la mossa. Le coppie dispari sono ininfluenti. Visto che la divisione dei pezzi in coppie è arbitraria, conviene fare scelte che semplifichino il calcolo, ad esempio formando quante più coppie dispari è possibile.
Nella posizione del Diagramma 1 si può scegliere di formare le coppie (1-9), (7-15) e (19-27). Sono tutte coppie dispari perché i due pezzi di ogni coppia sono separati da una casella. Quindi si hanno zero coppie pari: chi muove non ha la mossa.
Ma si possono fare scelte alternative e, per esempio, formare le coppie (1-9), (7-27) e (15-19). La coppia (1-9) è dispari. La coppia (7-27) è pari perché i due pezzi sono separati da quattro caselle. La coppia (15-19) è pari perché i due pezzi sono separati da zero caselle. Quindi si hanno due coppie pari: chi muove non ha la mossa.
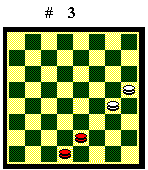
La mossa si inverte con un cambio. Portare "a spasso" pezzi per la damiera non ha alcun effetto. Se nella posizione del Diagramma 3 deve muovere il Bianco, non ha la mossa, ma può acquistarla con il cambio 20-23.
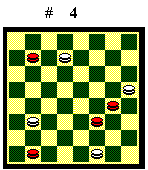
Con il baratto invece la mossa a
volte si inverte, a volte no. Se nella posizione del Diagramma 4
deve muovere il Bianco, ha anche la mossa. Con il baratto 31-27 (o 31-28)
la mossa non si inverte. Invece con il baratto 6-2, 29-25 la mossa si inverte
e passa al Nero.